文章目录
背景
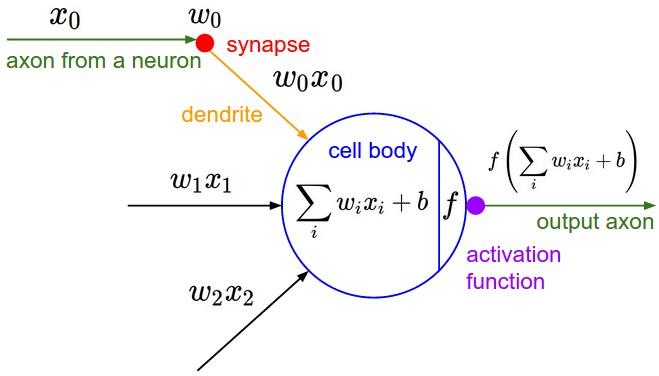
深度学习的基本原理是基于人工神经网络,信号从一个神经元进入,经过非线性的 activation function,传入到下一层神经元;再经过该层神经元的 activate,继续往下传递,如此循环往复,直到输出层。正是由于这些非线性函数的反复叠加,才使得神经网络有足够的 capacity 来抓取复杂的 pattern,在各个领域取得 state-of-the-art 的结果。显而易见,activation function 在深度学习中举足轻重,也是很活跃的研究领域之一。目前来讲,选择怎样的 activation function 不在于它能否模拟真正的神经元,而在于能否便于优化整个深度神经网络。下面我们简单聊一下各类函数的特点以及为什么现在优先推荐 ReLU 函数。
Sigmoid 函数
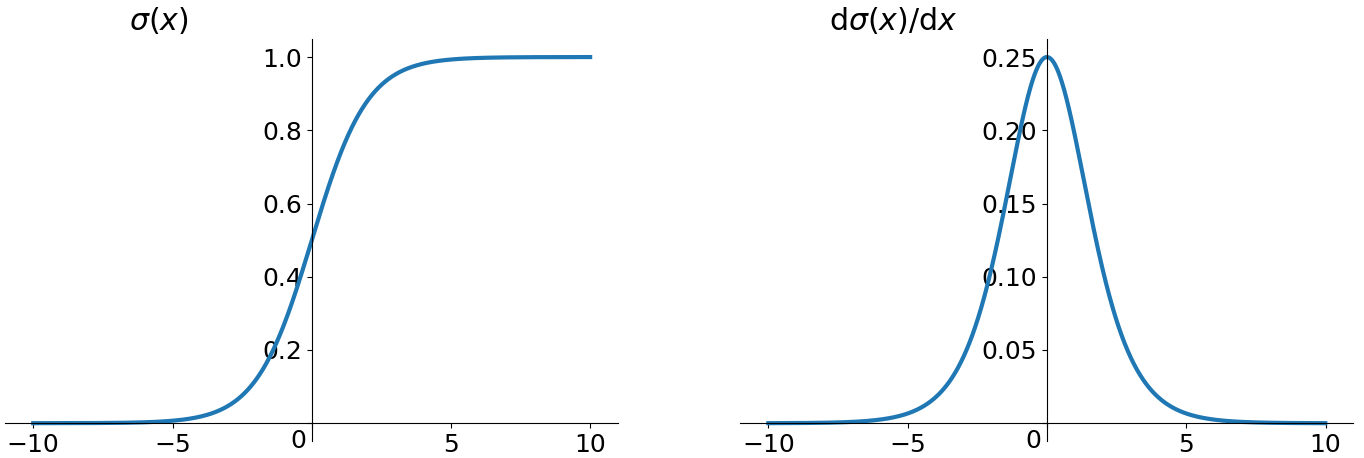
Sigmoid 函数是深度学习领域开始时使用频率最高的 activation function。它是便于求导的平滑函数,其导数为,这是优点。然而,Sigmoid 有三大缺点:
- 容易出现 gradient vanishing
- 函数输出并不是 zero-centered
- 幂运算相对来讲比较耗时
Gradient Vanishing
优化神经网络的方法是 Back Propagation,即导数的后向传递:先计算输出层对应的 loss,然后将 loss 以导数的形式不断向上一层网络传递,修正相应的参数,达到降低 loss 的目的。 Sigmoid 函数在深度网络中常常会导致导数逐渐变为 0,使得参数无法被更新,神经网络无法被优化。原因在于两点:(1) 在上图中容易看出,当 中 x 较大或较小时,导数接近 0,而后向传递的数学依据是微积分求导的链式法则,当前层的导数需要之前各层导数的乘积,几个小数的相乘,结果会很接近 0 (2) Sigmoid 导数的最大值是 0.25,这意味着导数在每一层至少会被压缩为原来的 1/4,通过两层后被变为 1/16,…,通过 10 层后为 1/1048576。请注意这里是 “至少”,导数达到最大值这种情况还是很少见的。
输出不是 zero-centered
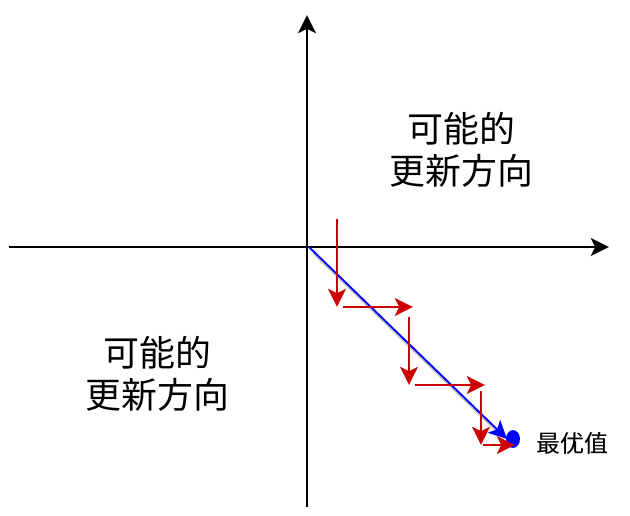
Sigmoid 函数的输出值恒大于 0,这会导致模型训练的收敛速度变慢。举例来讲,对,如果所有 * Xi 均为正数或负数,那么其对 Wi * 的导数总是正数或负数,这会导致如下图红色箭头所示的阶梯式更新,这显然并非一个好的优化路径。深度学习往往需要大量时间来处理大量数据,模型的收敛速度是尤为重要的。所以,总体上来讲,训练深度学习网络尽量使用 zero-centered 数据 (可以经过数据预处理实现) 和 zero-centered 输出。
幂运算相对耗时
相对于前两项,这其实并不是一个大问题,我们目前是具备相应计算能力的,但面对深度学习中庞大的计算量,最好是能省则省。之后我们会看到,在 ReLU 函数中,需要做的仅仅是一个 thresholding,相对于幂运算来讲会快很多。
tanh 函数
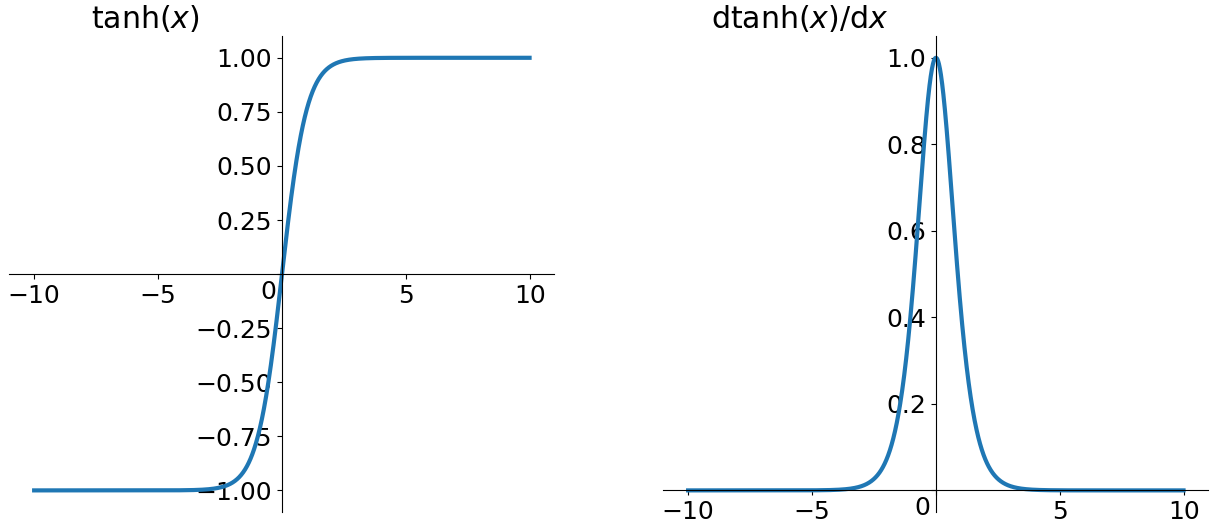
tanh 读作 Hyperbolic Tangent,如上图所示,它解决了 zero-centered 的输出问题,然而,gradient vanishing 的问题和幂运算的问题仍然存在。
ReLU 函数
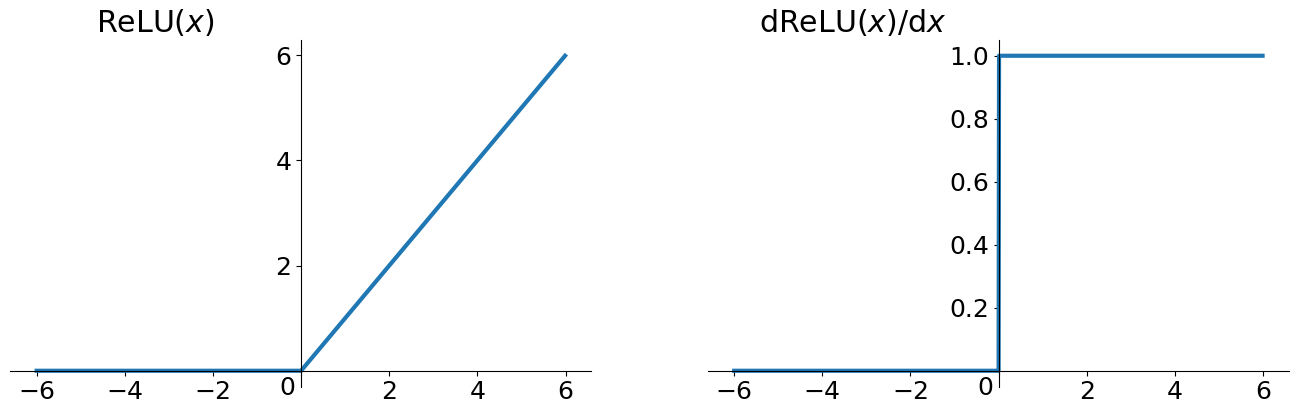
ReLU 函数其实就是一个取最大值函数,注意这并不是全区间可导的,但是我们可以取 sub-gradient,如上图所示。ReLU 虽然简单,但却是近几年的重要成果,有以下几大优点:
- 解决了 gradient vanishing 问题 (在正区间)
- 计算速度非常快,只需要判断输入是否大于 0
- 收敛速度远快于 sigmoid 和 tanh
ReLU 也有几个需要特别注意的问题:
-
ReLU 的输出不是 zero-centered
-
Dead ReLU Problem,指的是某些神经元可能永远不会被激活,导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生:
(1) 非常不幸的参数初始化,这种情况比较少见
(2) learning rate 太高导致在训练过程中参数更新太大,不幸使网络进入这种状态。解决方法是可以采用 Xavier 初始化方法,以及避免将 learning rate 设置太大或使用 adagrad 等自动调节 learning rate 的算法。
尽管存在这两个问题,ReLU 目前仍是最常用的 activation function,在搭建人工神经网络的时候推荐优先尝试!
Leaky ReLU 函数
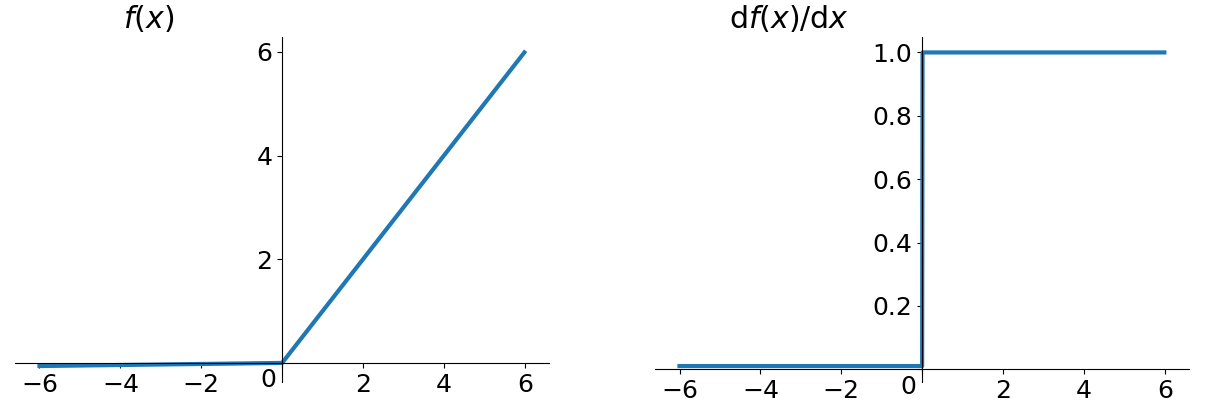
人们为了解决 Dead ReLU Problem,提出了将 ReLU 的前半段设为 0.01x 而非 0。另外一种直观的想法是基于参数的方法,即 Parametric ReLU:,其中 α 可由 back propagation 学出来。理论上来讲,Leaky ReLU 有 ReLU 的所有优点,外加不会有 Dead ReLU 问题,但是在实际操作当中,并没有完全证明 Leaky ReLU 总是好于 ReLU。
ELU (Exponential Linear Units) 函数
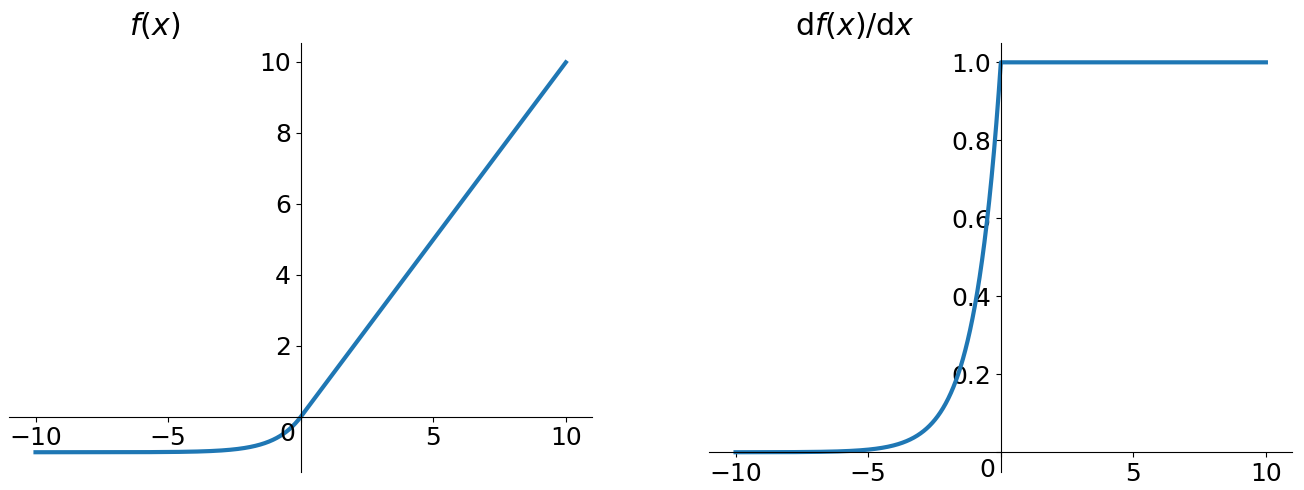
ELU 也是为解决 ReLU 存在的问题而提出,显然,ELU 有 ReLU 的基本所有优点,以及:
- 不会有 Dead ReLU 问题
- 输出的均值接近 0,zero-centered
它的一个小问题在于计算量稍大。类似于 Leaky ReLU,理论上虽然好于 ReLU,但在实际使用中目前并没有好的证据 ELU 总是优于 ReLU。
小结
建议使用 ReLU 函数,但是要注意初始化和 learning rate 的设置;可以尝试使用 Leaky ReLU 或 ELU 函数;不建议使用 tanh,尤其是 sigmoid 函数。
最后更新: 2021年07月15日 21:06

