文章目录
- 什么是损失函数?
- 一、Zero-one Loss(0-1 损失)
- 二、Hinge Loss
- 三、softmax-loss (多类别)
- 四、Logistic-loss(二分类的交叉熵损失函数)
- 五、交叉熵,cross entropy(多分类)
- 六、softmax cross entropy
- 七、triplet loss
- 八、均方误差(mean squared error,MSE)
- 九、平均绝对误差(Mean Absolute Error,MAE)
- 十、Smooth L1 损失
- 十一、center loss
什么是损失函数?
损失函数 (Loss Function) 也可称为代价函数 (Cost Function)或误差函数(Error Function),用于衡量预测值与实际值的偏离程度。一般来说,我们在进行机器学习任务时,使用的每一个算法都有一个目标函数,算法便是对这个目标函数进行优化,特别是在分类或者回归任务中,便是使用损失函数(Loss Function)作为其目标函数。机器学习的目标就是希望预测值与实际值偏离较小,也就是希望损失函数较小,也就是所谓的最小化损失函数。
损失函数是用来评价模型的预测值与真实值的不一致程度,它是一个非负实值函数。通常使用来表示,损失函数越小,模型的性能就越好。
一、Zero-one Loss(0-1 损失)
0-1 loss 是最原始的 loss,它是一种较为简单的损失函数,如果预测值与目标值不相等,那么为 1,否则为 0,即:
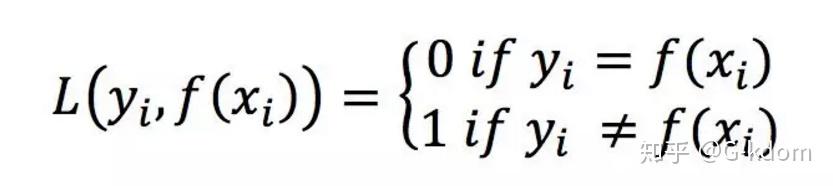
0-1 损失可用于分类问题,但是由于该函数是非凸的,在最优化过程中求解不方便,有阶跃,不连续。0-1 loss 无法对 x 进行求导,在依赖于反向传播的深度学习任务中,无法被使用,所以使用不多。
二、Hinge Loss
Hinge loss 主要用于支持向量机(SVM)中,它的称呼来源于损失的形状,定义如下:
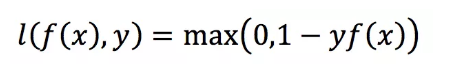
其中 y=+1 或−1,f (x)=wx+b,当为 SVM 的线性核时。如果分类正确,loss=0,如果错误则为 1-f (x),所以它是一个分段不光滑的曲线。Hinge loss 被用来解 SVM 中的间隔最大化问题。
三、softmax-loss (多类别)
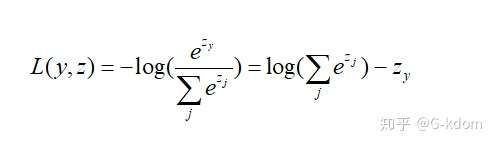
其中主要是 softmax 函数计算的类别概率。softmax loss 被广泛用于分类问题中,而且发展出了很多的变种,有针对不平衡样本问题的 weighted softmax loss、focal loss,针对蒸馏学习的 soft softmax loss,促进类内更加紧凑的 L-softmax Loss 等一系列改进。
强调一下 :softmax 函数与 softmax-loss 函数是不一样的,千万,千万别记混了。
softmax 函数最常用作分类器的输出,来表示 个不同类上的概率分布。
softmax 公式如下:
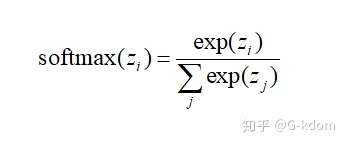
使用 softmax 分类的前提:类别之间都是相互独立的。
softmax 分类的本质:将特征向量做归一化处理(输出总是和为 1),将线性预测值转换为类别概率。
四、Logistic-loss(二分类的交叉熵损失函数)
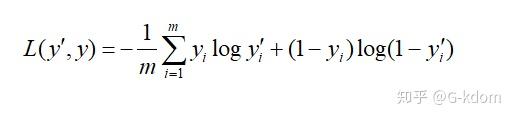
Logistic 不使用平方损失的原因:平方损失会导致损失函数是非凸的,不利于求解,因为非凸函数会存在许多的局部最优解。
五、交叉熵,cross entropy(多分类)
cross entropy loss 用于度量两个概率分布之间的相似性。
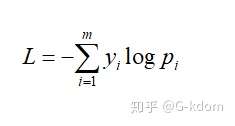
其中为样本的真实标签,取值只能为 0 或 1;为预测样本属于类别的概率;为类别的数量。
六、softmax cross entropy
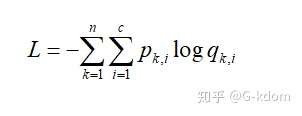
其中 Pk,i 表示样本 k 属于类别 i 的概率(真实标签,只能为 0 或 1);qk,i 表示 softmax 预测的样本 k 属于类别 i 的概率;c 是类别数;n 是样本总数。如果概率是通过 softmax 计算得到的,那么就是 softmax cross entropy。
七、triplet loss
triplet-loss 是深度学习中的一种损失函数,用于训练差异性较小的样本,如人脸等。数据包括锚(Anchor)示例、正(Positive)示例、负(Negative)示例,通过优化锚示例与正示例的距离小于锚示例与负示例的距离,实现样本的相似性计算。也就是说通过学习后,使得同类样本的 positive 更靠近 Anchor,而不同类的样本 Negative 则远离 Anchor。
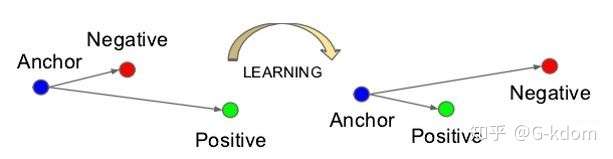
如上图所示,triplet 是一个三元组,这个三元组是这样构成的:从训练数据集中随机选一个样本,该样本称为 Anchor,然后再随机选取一个与 Anchor (记为 x_a) 属于同一类的样本和不同类的样本,这两个样本对应的称为 Positive (记为 x_p) 和 Negative (记为 x_n),由此构成一个(Anchor,Positive,Negative)三元组。
有了上面的 triplet 的概念, triplet loss 就好理解了。针对三元组中的每个元素(样本),训练一个参数共享或者不共享的网络,得到三个元素(样本)的特征表达,分别记为:
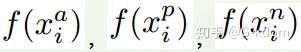
通过 Triplet Loss 的学习后,使得 Positive 和 Anchor(同类)特征表达之间的距离尽可能小,而 Anchor 和 Negative(不同类)特征表达之间的距离尽可能大,并且要让 x_a 与 x_n 之间的距离和 x_a 与 x_p 之间的距离之间有一个最小的间隔。公式表示就是:
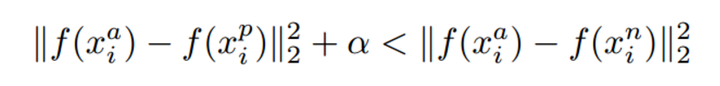
其中距离用欧式距离度量,α 也称为 margin(间隔)参数。设置一个合理的 margin 值很关键,这是衡量相似度的重要指标。简而言之,margin 值设置的越小,loss 很容易趋近于 0 ,但很难区分相似的图像。margin 值设置的越大,loss 值较难趋近于 0,甚至导致网络不收敛,但可以较有把握的区分较为相似的图像。
对应的目标函数为:
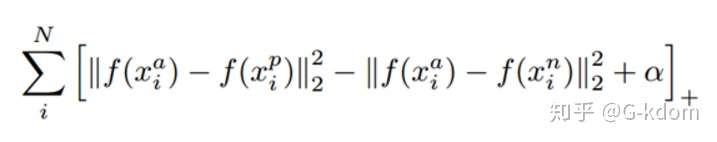
其中 + 表示 [ ] 内的值大于零的时候,取该值为损失;小于零的时候,损失为零。
【triplet loss 梯度推导】
我们将上述目标函数记为 L ,则有:
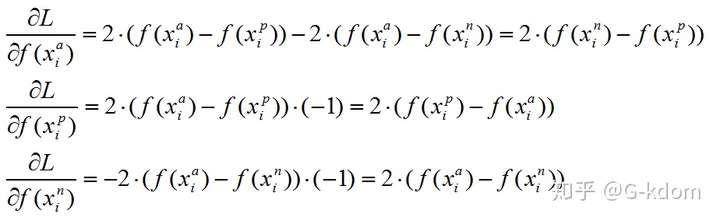
在训练 Triplet Loss 模型时,只需要输入样本,不需要输入标签,这样避免标签过多、同标签样本过少的问题,模型只关心样本编码,不关心样本类别。Triplet Loss 在相似性计算和检索中的效果较好,可以学习到样本与变换样本之间的关联,检索出与当前样本最相似的其他样本。Triplet Loss 通常应用于个体级别的细粒度识别,比如分类猫与狗等是大类别的识别,但是有些需求要精确至个体级别,比如识别不同种类不同颜色的猫等,所以 Triplet Loss 最主要的应用也是在细粒度检索领域中。
Triplet Loss 的优点:
如果把不同个体作为类别进行分类训练,Softmax 维度可能远大于 Feature 维度,精度无法保证。
Triplet Loss 一般比分类能学习到更好的特征,在度量样本距离时,效果较好;
Triplet Loss 支持调整阈值 Margin,控制正负样本的距离,当特征归一化之后,通过调节阈值提升置信度。
八、均方误差(mean squared error,MSE)
也叫平方损失或 L2 损失,常用在最小二乘法中。它的思想是使得各个训练点到最优拟合线的距离最小(平方和最小)。均方误差损失函数也是我们最常见的损失函数了,相信大家都很熟悉了,常用于回归问题中。定义如下:
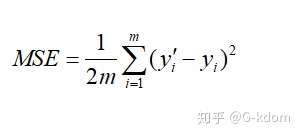
当预测值与目标值相差很大时,梯度容易爆炸,这既是 L2 loss 的最大问题。
九、平均绝对误差(Mean Absolute Error,MAE)
所有单个观测值与算术平均值的绝对值的平均,也被称为 L1 loss,常用于回归问题中。与平均误差相比,平均绝对误差由于离差被绝对值化,不会出现正负相抵消的情况,因而,平均绝对误差能更好地反映预测值误差的实际情况。
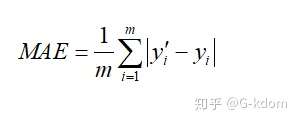
由于 L1 loss 具有稀疏性,为了惩罚较大的值,因此常常将其作为正则项添加到其他 loss 中作为约束。L1 loss 的最大问题是梯度在零点不平滑,导致会跳过极小值。
十、Smooth L1 损失
原始的 L1 loss 和 L2 loss 都有缺陷,比如 L1 loss 的最大问题是梯度不平滑,而 L2 loss 的最大问题是容易梯度爆炸,所以研究者们对其提出了很多的改进。
在 faster rcnn 框架中,使用了 smooth L1 loss 来综合 L1 与 L2 loss 的优点,定义如下:
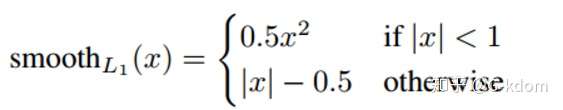
在比较小时,上式等价于 L2 loss,保持平滑。
在比较大时,上式等价于 L1 loss,可以限制数值的大小。Smooth L1 损失能够解决梯度爆炸问题。
十一、center loss
center loss 来自 ECCV2016 的一篇论文:A Discriminative Feature Learning Approach for Deep Face Recognition。
论文链接:http://ydwen.github.io/papers/WenECCV16.pdf
代码链接:https://github.com/pangyupo/mxnet_center_loss
什么是 center loss?一个 batch 中的每个样本的 feature 离 feature 的中心的距离的平方和要越小越好,也就是类内(intra-class)距离要越小越好。这就是 center loss。
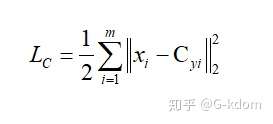
其中 m 表示 mini-batch 的大小,Xi 表示第 i 个样本的特征,Cyi 表示第 i 个正确样本的特征中心。
通常在用 CNN 做人脸识别等分类问题时,我们一般采用 softmax loss,在 close-set 测试中模型性能良好,但在遇到 unseen 数据情况下,模型性能会急剧下降。一个直观的感觉是:如果模型学到的特征判别度更高,那么再遇到 unseen 数据时,泛化性能会比较好。为了使得模型学到的特征判别度更高,论文提出了一种新的辅助损失函数,之说以说是辅助损失函数是因为新提出的损失函数需要结合 softmax loss,而非替代后者,在不同数据及上提高了识别准确率。
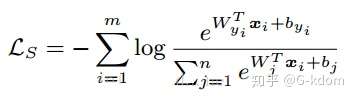
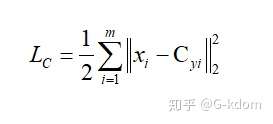
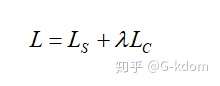
在结合使用这两种损失函数时,可以认为 softmax loss 负责增加 inter-class 距离,center-loss 负责减小 intra-class 距离,这样学习到的特征判别度会更高。
缺点 :最麻烦的地方在于如何选择训练样本对。在论文中,作者也提到了,选取合适的样本对对于模型的性能至关重要,论文中采用的方法是每次选择比较难以分类的样本对重新训练,类似于 hard-mining。同时,合适的训练样本还可以加快收敛速度。

