【详解】IoU、GIoU、DIoU、CIoU损失函数

---

文章目录

• 一、IOU (Intersection over Union)
• 二、GIOU (Generalized Intersection over Union)
• 三、DIoU (Distance-IoU)
• 四、CIoU (Complete-IoU)
• 五、损失函数在 YOLOv3 上的性能 (论文效果)

---

一、IOU (Intersection over Union)

1. 特性 (优点)

IoU 就是我们所说的交并比，是目标检测中最常用的指标，在 anchor-based 的方法中，他的作用不仅用来确定正样本和负样本，还可以用来评价输出框（predict box）和 ground-truth 的距离。

1. 可以说它可以反映预测检测框与真实检测框的检测效果。
2. 还有一个很好的特性就是尺度不变性，也就是对尺度不敏感（scale invariant）， 在 regression 任务中，判断 predict box 和 gt 的距离最直接的指标就是 IoU。(满足非负性；同一性；对称性；三角不等性)

import numpy as np
def Iou(box1, box2, wh=False):
    if wh == False:
	xmin1, ymin1, xmax1, ymax1 = box1
	xmin2, ymin2, xmax2, ymax2 = box2
    else:
	xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
	xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
	xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)
	xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)
    # 获取矩形框交集对应的左上角和右下角的坐标（intersection）
    xx1 = np.max([xmin1, xmin2])
    yy1 = np.max([ymin1, ymin2])
    xx2 = np.min([xmax1, xmax2])
    yy2 = np.min([ymax1, ymax2])	
    # 计算两个矩形框面积
    area1 = (xmax1-xmin1) * (ymax1-ymin1) 
    area2 = (xmax2-xmin2) * (ymax2-ymin2)
    inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))　#计算交集面积
    iou = inter_area / (area1+area2-inter_area+1e-6) 　#计算交并比

    return iou

2. 作为损失函数会出现的问题 (缺点)

1. 如果两个框没有相交，根据定义，IoU=0，不能反映两者的距离大小（重合度）。同时因为 loss=0，没有梯度回传，无法进行学习训练。
2. IoU 无法精确的反映两者的重合度大小。如下图所示，三种情况 IoU 都相等，但看得出来他们的重合度是不一样的，左边的图回归的效果最好，右边的最差。

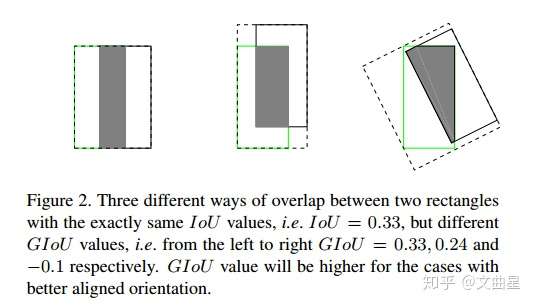
二、GIOU (Generalized Intersection over Union)

1、来源

在 CVPR2019 中，论文

《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》arxiv.org/abs/1902.09630

的提出了 GIoU 的思想。由于 IoU 是比值的概念，对目标物体的 scale 是不敏感的。然而检测任务中的 BBox 的回归损失 (MSE loss, l1-smooth loss 等）优化和 IoU 优化不是完全等价的，而且 Ln 范数对物体的 scale 也比较敏感，IoU 无法直接优化没有重叠的部分。

这篇论文提出可以直接把 IoU 设为回归的 loss。

• GIoU 对 scale 不敏感
• GIoU 是 IoU 的下界，在两个框无限重合的情况下，IoU=GIoU=1
• IoU 取值 [0,1]，但 GIoU 有对称区间，取值范围 [-1,1]。在两者重合的时候取最大值 1，在两者无交集且无限远的时候取最小值 - 1，因此 GIoU 是一个非常好的距离度量指标。
• 与 IoU 只关注重叠区域不同，GIoU 不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度。

def Giou(rec1,rec2):
    #分别是第一个矩形左右上下的坐标
    x1,x2,y1,y2 = rec1 
    x3,x4,y3,y4 = rec2
    iou = Iou(rec1,rec2)
    area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
    area_1 = (x2-x1)*(y1-y2)
    area_2 = (x4-x3)*(y3-y4)
    sum_area = area_1 + area_2

    w1 = x2 - x1   #第一个矩形的宽
    w2 = x4 - x3   #第二个矩形的宽
    h1 = y1 - y2
    h2 = y3 - y4
    W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)    #交叉部分的宽
    H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)    #交叉部分的高
    Area = W*H    #交叉的面积
    add_area = sum_area - Area    #两矩形并集的面积

    end_area = (area_C - add_area)/area_C    #闭包区域中不属于两个框的区域占闭包区域的比重
    giou = iou - end_area
    return giou

三、DIoU (Distance-IoU)

1、来源

DIoU 要比 GIou 更加符合目标框回归的机制，将目标与 anchor 之间的距离，重叠率以及尺度都考虑进去，使得目标框回归变得更加稳定，不会像 IoU 和 GIoU 一样出现训练过程中发散等问题。论文中

Distance-IoUarxiv.org/pdf/1911.08287.pdf

基于 IoU 和 GIoU 存在的问题，作者提出了两个问题：

1. 直接最小化 anchor 框与目标框之间的归一化距离是否可行，以达到更快的收敛速度？

2. 如何使回归在与目标框有重叠甚至包含时更准确、更快？

其中，b, b^gt 分别代表了预测框和真实框的中心点，且 ρ 代表的是计算两个中心点间的欧式距离。 c 代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。

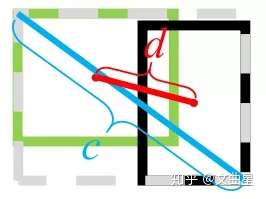
DIoU 中对 anchor 框和目标框之间的归一化距离进行了建模

附：

YOLOV3 DIoU GitHub 项目地址：github.com/Zzh-tju/DIoU-darknet

2、优点

• DIoU loss 可以直接最小化两个目标框的距离，因此比 GIoU loss 收敛快得多。
• 对于包含两个框在水平方向和垂直方向上这种情况，DIoU 损失可以使回归非常快，而 GIoU 损失几乎退化为 IoU 损失。
• DIoU 还可以替换普通的 IoU 评价策略，应用于 NMS 中，使得 NMS 得到的结果更加合理和有效。

实现代码：

def Diou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    dious = torch.zeros((rows, cols))
    if rows * cols == 0:#
        return dious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        dious = torch.zeros((cols, rows))
        exchange = True
    # #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1] 
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]
    
    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2 
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2 
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:]) 
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2]) 
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:]) 
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    dious = inter_area / union - (inter_diag) / outer_diag
    dious = torch.clamp(dious,min=-1.0,max = 1.0)
    if exchange:
        dious = dious.T
    return dious

四、CIoU (Complete-IoU)

实现代码：

def bbox_overlaps_ciou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    cious = torch.zeros((rows, cols))
    if rows * cols == 0:
        return cious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        cious = torch.zeros((cols, rows))
        exchange = True

    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1]
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]

    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    u = (inter_diag) / outer_diag
    iou = inter_area / union
    with torch.no_grad():
        arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
        v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
        S = 1 - iou
        alpha = v / (S + v)
        w_temp = 2 * w1
    ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
    cious = iou - (u + alpha * ar)
    cious = torch.clamp(cious,min=-1.0,max = 1.0)
    if exchange:
        cious = cious.T
    return cious

五、损失函数在 YOLOv3 上的性能 (论文效果)

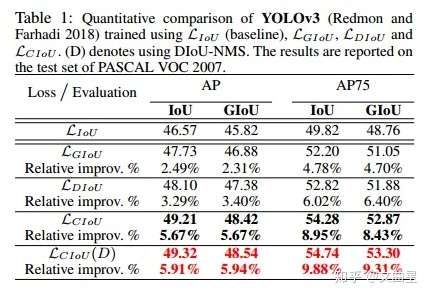
目标检测算法之 AAAI 2020 DIoU Loss 已开源 (YOLOV3 涨近 3 个点)：cloud.tencent.com/developer/article/1558533

最后更新： 2021年08月28日 16:50

原始链接： https://leezhao415.github.io/2021/08/28/%E3%80%90%E8%AF%A6%E8%A7%A3%E3%80%91IoU%E3%80%81GIoU%E3%80%81DIoU%E3%80%81CIoU%E6%8D%9F%E5%A4%B1%E5%87%BD%E6%95%B0/

LeeZhao

赏

× 请我吃糖~